Strength of Materials - Strains
|
3.
Strains
Strain is defined a the ratio of change in
dimension to original dimension of a body when
it is deformed. It is a dimensionless quantity
as it is a ratio between two quantities of same
dimension.
|
|
3.1.
Linear Strain
Linear strain of a deformed body is defined as
the ratio of the change in length of the body
due to the deformation to its original length
in the direction of the force. If l is the original
length and dl the change in length occurred due
to the deformation, the linear strain e induced
is given by e=dl/l.
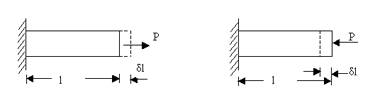
Linear strain may be a tensile strain, et
or a compressive strain ec
according as dl refers to an increase in length
or a decrease in length of the body. If we consider
one of these as +ve then the other should be
considered as –ve, as these are opposite
in nature.
|
| |
| 3.2.
Lateral Strain
Lateral strain of a deformed body is defined as
the ratio of the change in length (breadth of
a rectangular bar or diameter of a circular bar)
of the body due to the deformation to its original
length (breadth of a rectangular bar or diameter
of a circular bar) in the direction perpendicular
to the force. |
| |
|
| |
3.3. Volumetric
Strain
Volumetric strain of a
deformed body is defined as the ratio of the
change in volume of the body to the deformation
to its original volume. If V is the original
volum and dV the change in volume occurred due
to the deformation, the volumetric strain ev
induced is given by ev =dV/V
Consider a uniform rectangular bar of length
l, breadth b and depth d as shown in figure.
Its volume V is given by,
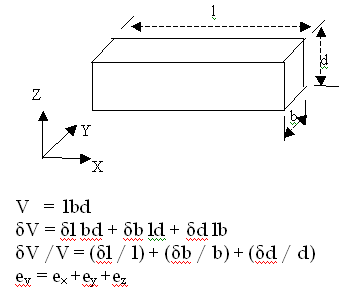
This means that volumetric
strain of a deformed body is the sum of the
linear strains in three mutually perpendicular
directions.
|
| |
3.4.
Shear Strain
Shear strain is
defined as the strain accompanying a shearing
action. It is the angle in radian measure through
which the body gets distorted when subjected to
an external shearing action. It is denoted by
*.
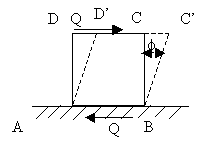
Consider a cube ABCD subjected
to equal and opposite forces Q across the top
and bottom forces AB and CD. If the bottom face
is taken fixed, the cube gets distorted through
angle * to the shape ABC’D’. Now strain
or deformation per unit length is
Shear strain of cube = CC’ / CD = CC’
/ BC = * radian
|
| |
|