|
|
| |
Strength of Materials - Poisson’s
Ratio
|
| 5.
Poisson’s Ratio
Any direct stress is accompanied by a strain in
its own direction and called linear strain and
an opposite kind strain in every direction at
right angles to it, lateral strain. This lateral
strain bears a constant ratio with the linear
strain. This ratio is called the Poisson’s
ratio and is denoted by (1/m) or µ.
Poisson’s Ratio = Lateral Strain / Linear
Strain.
Value of the Poisson’s ratio for most materials
lies between 0.25 and 0.33. |
| |
6.
Complementary Strain
Consider
a rectangular element ABCD of a body subjected
to simple shear of intensity q as shown. Let t
be the thickness of the element. Total force on
face AB is , FAB = stress X area = q X AB X t.
Total force on face CD is, FCD = q X CD Xt = q
XAB Xt.
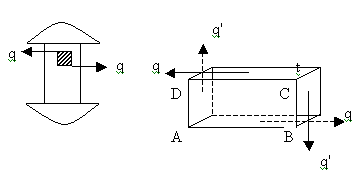
FAB and FCD being equal and opposite, constitute
a couple whose moment is given by,
M =FAB X BC = q XAB X BC X t
Since the element is in equilibrium within the
body, there must be a balancing couple which can
be formed only by another shear stress of some
intensity q’ on the faces BC and DA. This
shear stress is called the complementary stress.
FBC = q’ X BC X t
FDA = q’ X DA X t = q’ X BC Xt
The couple formed by these two forces is M’
= FBC X AB = q’ X BC X t
For equilibrium, M’ = M.
Therefore q’ = q
This enables us to make the following statement.
In a state of simple shear a shear stress of any
intensity along a plane is always accompanied
by a complementary shear stress of same intensity
along a plane at right angles to the plane.
|
| |
|
| |
7.
Direct Stresses Developed Due to Simple Shear.
Consider a square element of side a and thickness
t in a state of simple shear as shown in figure.
It is clear that the shear stress on the forces
of element causes it to elongate in the direction
of the diagonal BD. Therefore a tensile stress
of same intensity pt is induced in the elements
along BD. ie, across the plane of the diagonal
AC. The triangular portion ABC of the element
is in equilibrium under the action of the following.
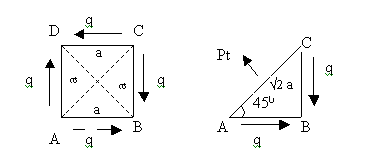
(1)FAC = Normal force on face AC = pt X AC X t
= pt X v2 aXt
(2)FAB = Tangential force on face AB = q X BC
X t = q aXt
(3)FBC = Tangential force on face BC = q X BC
X t = q aXt
For equilibrium in the direction normal to AC,
FAC – FAB cos45 – FBC cos45 = 0
Pt X v2 at – q at X 1/v2 - q at X 1/v2 =
0
v2 pt – 2 q /v2 = 0
pt = q
It can also be seen that the shear stress on the
faces of the element causes it to foreshorten
in the direction of the diagonal BD. Therefore
a compressive stress pc is induced in the element
in the direction AC, ie across the plane of the
diagonal BD. It can also be shown that pc = q.
It can thus be concluded that simple shear of
any intensity gives rise to direct stresses of
same intensity along the two planes inclined at
45º to the shearing plane. The stress along
one of these planes being tensile and that along
the other being compressive. |
| |
|
|
|
|
|
|