|
|
| |
Strength of Materials - Relationship
among the elastic constants
|
| 8.1.
Relationship between modulus of elasticity and
modulus of rigidity
Consider a square element ABCD of side ‘a’
subjected to simple shear of intensity q as shown
in figure.
It is deformed to the shape AB’C’D
under the shear stress. Drop perpendicular BE
to the diagonal DB’. Let ? be the shear
strain induced and let N be the modulus of rigidity.
The diagonal DB gets elongated to DB’. Hence
there is tensile strain et in the diagonal.
et = (DB’ – DB) / DB = EB’ /
DB
since this deformation is very small we can take
L BB’E = 45º
EB’ = BB’ / v2 = AB tan ? / v2 = a
tan ? / v2
DB = v2 a
et = (a tan ? / v2)/ v2 a = tan ? /2 = = ? / 2
since ? is small
ie et = ½ X q/N ------------------ (1)
We know that stress along the diagonal DB is a
pure tensile stress pt = q and that along the
diagonal AC is a pure compressive stress pc also
equal to q. hence the strain along the diagonal
DB is et = q/E + 1/m X q/E
Ie et = q/E (1+1/m) ------------------ (2)
From (1) and (2) we have,
E = 2N(1+1/m)
This is the required relationship between E and
N.
|
| |
|
|
| |
8.2.
Relationship between Modulus of Elasticity E and
Bulk Modulus K
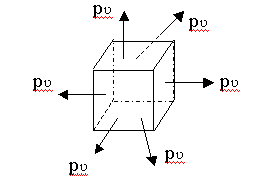
Consider a cube element subjected to volumetric
tensile stress p? in X,Y and Z directions. Stress
in each direction is equal to p?. ie px = py =
pz =p?
Consider strains induced in X-direction by these
stresses. px induces tensile strain , while py
and pz induces compressive strains. Therefore,
ex = px/E – 1/m[py/E + pz/E] = p?/E[1-2/m]
due to the perfect symmetry in geometry and stresses
ey = p?/E[1-2/m]
ez = p?/E[1-2/m]
K = p ? / e ? =p ?/(ex+ey+ez) = p?/[3p?/E(1-2/m)]
ie E = 3K(1-2/m ) is the required relationship.
|
| |
|
| |
8.3.
Relationship among the constants
From above,
E = 2N[1+(1/m)] and E = 3K[1-(2/m )]
E = 3K[1-2(E/2N -1)] = 3K[1-E/N +2]
9K = E[1+(3K/N)] = E[(N+3K)/N]
E = 9NK/(N+3K)
9. Bars of uniform
section
Consider a bar of length l and Cross sectional
area A. Let P be the axial pull on the bar,p the
stresss induced ,e the strain in the bar and dl
is the elongation.
Then p= P/A
e= p/E =P/(AE) -------------(1)
e= dl/l -------------(2)
equating (1) and (2)
dl = Pl / (AE) |
|
|
| |
| You
can download these notes by clicking here
|
| |
|
|
|